NFA to DFA Algorithm:

Dstates := {å_closure(start_state)}

while T := unmarked_member(Dstates) do {

mark(T)

for each input symbol a do {

U :=å_closure(move(T,a))

if not member(Dstates, U) then

insert(Dstates, U)

Dtran[T,a] := U

}

}

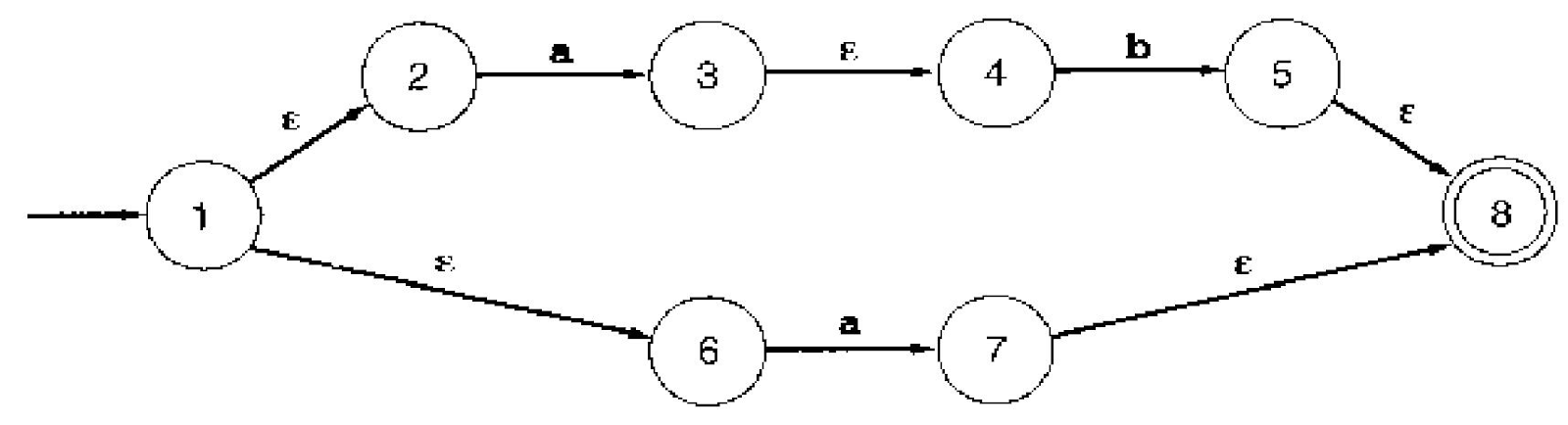
Practice converting NFA to DFA

OK, you've seen the algorithm, now can you use it?

...

...did you get:

OK, how about this one:

Some Remarks

· If you checked out the class web page, you saw a solution to HW#1 was posted awhile

ago... I will try to do this for future assignments also, but can't do so very promptly if I

wish to have a relaxed "late turnin" policy. What is in your best interests?

· Color BASIC has two-letter identifiers. We are doing Extended Color BASIC, so we will

allow longer identifier names. But in the current assignment #2 you will only be tested

on short variable names.

· Whether we return the same or a different category for integer constants and for line

numbers depends very much on the grammar we use to parse BASIC, and whether it can

understand what's going on with the line numbers if it doesn't have two categories. My

instinct tells me we will probably need either a token for newline characters or will need

to detect line numbers as distinct from normal integer constants. Before we can answer

that question, we need to learn about syntax!

Lexical Analysis and the Literal Table

In many compilers, the memory management components of the compiler interact with several

phases of compilation, starting with lexical analysis.

· Efficient storage is necessary to handle large input files.

· There is a colossal amount of duplication in lexical data: variable names, strings and

other literal values duplicate frequently

· What token type to use may depend on previous declarations.

A hash table or other efficient data structure can avoid this duplication. The software

engineering design pattern to use is called the "flyweight".

Major Data Structures in a Compiler

token

contains an integer category, lexeme, line #, column #, filename... We could build these

into a link list, but instead we'll use them as leaves in a tree structure.

syntax tree

contains grammar information about a sequence of related tokens. leaves contain

lexical information (tokens). internal nodes contain grammar rules and pointers to

tokens or other tree nodes.

symbol table

contains variable names, types, and information needed to generate code for a name

(such as its address, or constant value). Look ups are by name, so we'll need a hash

table.

intermediate& final code

We'll need link lists or similar structures to hold sequences of machine instructions

Literal Table: Usage Example

Example abbreviated from [ASU86]: Figure 3.18, p. 109. Use "install_id()" instead of

"strdup()" to avoid duplication in the lexical data.

%{

/* #define's for token categories LT, LE, etc.

%}

white [ \t\n]+

digit [0-9]

id [a-zA-Z_][a-zA-Z_0-9]*

num {digit}+(\.{digit}+)?

%%

{ws} { /* discard */ }

if { return IF; }

then { return THEN; }

else { return ELSE; }

{id} { yylval.id = install_id(); return ID; }

{num} { yylval.num = install_num(); return NUMBER; }

"<" { yylval.op = LT; return RELOP; }

">" { yylval.op = GT; return RELOP; }

%%

install_id()

{

/* insert yytext into the literal table */

}

install_num()

{

/* insert (binary number corresponding to?) yytext into the literal table */

}

So how would you implement a literal table using a hash table? We will see more hash tables

when it comes time to construct the symbol tables with which variable names and scopes are

managed, so you had better become fluent.